
ブログをNext.js14(App Router)でリファクタリングしました

この記事ではN次元空間における「超曲面と等高線(等値面)の法線ベクトル」の公式について、図と例を用いて直感的に分かりやすく説明しています。大学の初等数学が分かれば読める内容となっています。これが理解できれば、ラグランジュの未定乗数法や機械学習にも応用できます。
この記事では以下のような大学数学の概念が登場します。
これらについてご存知ない方は、以下の記事をご覧ください。短時間で学べます。
①N次元ベクトルについて
②N変数関数と偏微分について
N変数からなる関数をN次元ベクトルxを用いて
と表記したとき、
N次の超曲面
(陰関数表示)一般的にNが2次元のときは曲線、Nが3次元のときは曲面、Nが4次元以上の時に超曲面と言います。
つまりN変数関数の陰関数表示、N-1変数関数の陽関数表示はN次元の超曲面を表します。
ちなみに直線や平面も曲面の一種です。
陽関数
は2次曲線を表します。
陽関数は陰関数に変換することができ、
の形に式変形すると
と表せます。
という の形の関数を陽関数、 の形のものを陰関数というのでした。同じ関数を表しますが、変数の数が異なる点に注意して下さい。
陽関数の超曲面が「同じ値となる場所に描いた線」を等高線といいます。(厳密には3次元以上のときは等値面といいます。)
山の地図に出てくる等高線と同じです。地図の等高線は山の同じ高さの部分に線を引いたものですが、数学的には山の高さがz座標となり、
が同じ高さとなるx-y平面上の線を表しています。
3次元の山を2次元の地図で表せたように、等高線は実際より低次元空間で超曲面を表現するのに役立ちます。
数式でN次元の場合に一般化すると、constを任意の定数として次のように書けます。
等高線
N変数関数の等高線は、陽関数表示を用いて3次元における例を挙げます。
の放物面(放物線のN次元版)があったとき、等高線は次の図のようになります。
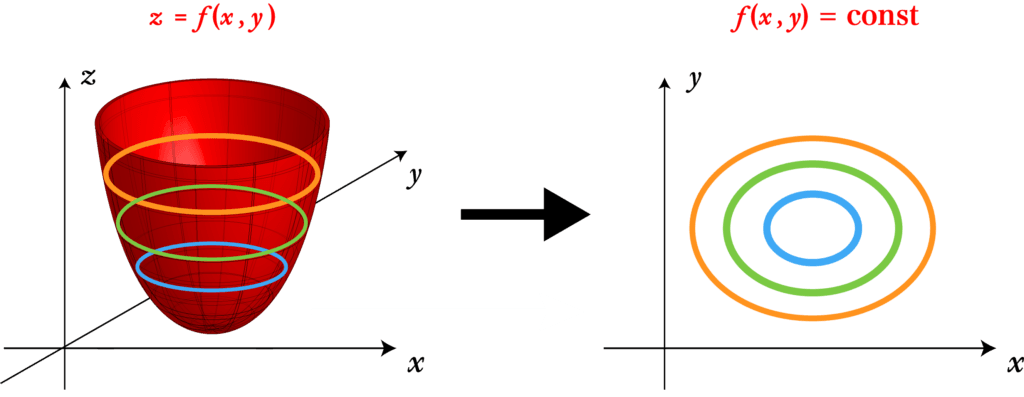
等高線を図で書く場合は、等高線を適当に数本ピックアップして図示します。
上の図は3次元の放物面の等高線をx-y平面に図示したものとなります。
例えば、z=20になる部分のx-y平面上の線(水色)、z=40となる線(緑)、z=60(オレンジ)となる線の三本を書きます。
それでは次に法線ベクトルの定義について説明していきます。
をn次元ベクトルとします。 このとき、陰関数表示の超曲面 の法線ベクトルnは次のようになります。
超曲面の法線ベクトル
が陰関数のときこの定義を2次元で理解しましょう。
2次元なので、関数 の変数を、2変数 とします。
曲線 上の近接する2点 を考え、 とします。
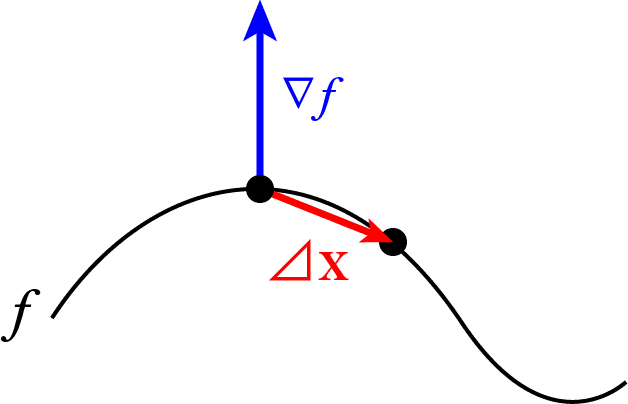
これらの点は曲線 上にあるので、
2変数のテイラー展開の公式、
において、
(:=は代入を表す)とすると
となるから
として②の式をテイラー展開すると、
よって
とすれば、高次の項を無視できるので
となります。
内積が0ということは垂直に交わっているので、図のように
は法線ベクトルとなります。
は非常にミクロの世界、つまり曲線が直線とみなせるほど拡大した場合に
と直行しているので、曲線と直行しているとみなすことが出来ます。
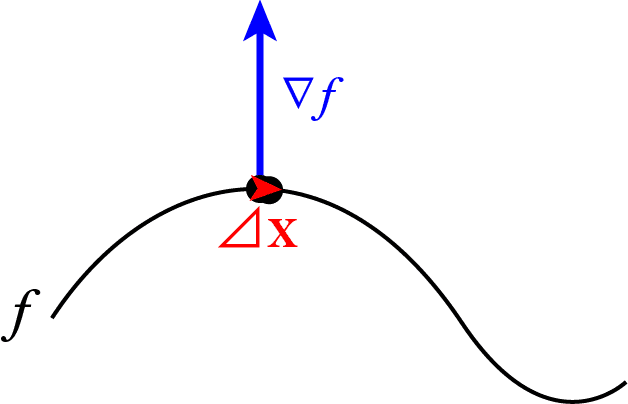
このように2次元で公式の意味をイメージできれば、高次元においても成り立つことが想像できるでしょう。
超曲面の法線ベクトルが分かれば同じ要領です。
等高線(等値面)の法線ベクトルの公式は以下のとおりです。
超曲面の等高線の法線ベクトル
が陽関数のとき、3次元の曲面 で考えましょう。
等高線は、同じ高さzを取る場所を線にして表したものです。
constを定数という意味で使うと、任意の等高線は
と表せ、2次元平面上で曲線として描くことができます。
この等高線上の2点
を考えます。
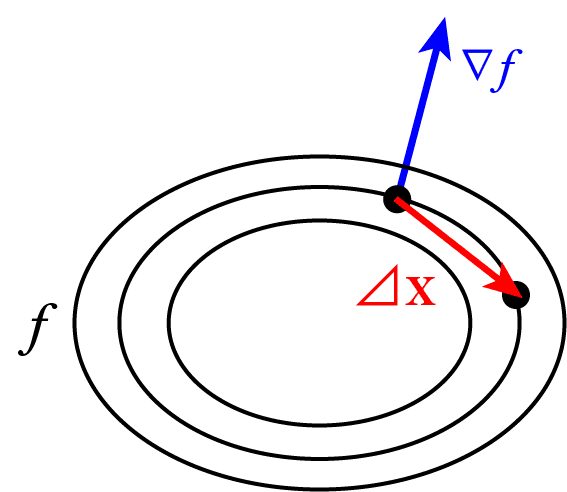
これらの2点は
となり、⑤式をテイラー展開すると
あとは先程と同様に、
とすれば、高次の項を無視できるので
となります。
内積が0ということは垂直に交わっているので、図のように
は法線ベクトルとなります。
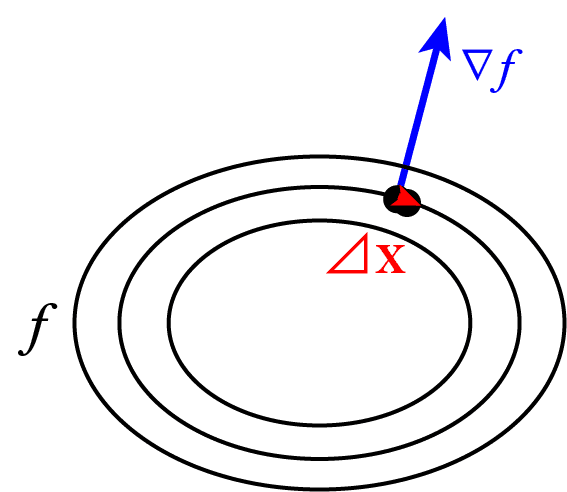
超曲面も等高線も、その勾配が法線ベクトルとなることを解説しました。
この概念は機械学習の中でも様々な場面で利用する基本の公式となります。
特に等高線の法線ベクトルに関しては、続き記事になる「ラグランジュの未定乗数法」で利用しています。
続きの記事
最新の記事
カテゴリー一覧
アーカイブ