多変数のラグランジュの未定乗数法と2次計画問題

ラグランジュの未定乗数法は「ある条件下で関数の極値を求める」方法です。2変数で等式制約のケースの解き方は大学の初等数学で習いますが、3次元以上の「多変数」の場合や「不等式制約」におけるラグランジュの未定乗数法は、実際に応用されている場所で初めて出くわすかもしれません。

この記事では「多変数・N変数のラグランジュの未定乗数法」とその解き方を、「等式制約」の場合と「不等式制約」の場合に分けて解説します。さらに「不等式制約」について2次計画問題と呼ばれるものについて説明します。

はじめに

前提となる知識

• N変数(多変数)の関数とその偏微分・勾配
• N次元ベクトルとその性質
• 超曲面や等高線の法線ベクトル

それぞれ以下の記事から短時間で学べます。

①N次元ベクトルについて

②N変数関数と偏微分について

③超曲面や法線ベクトルについて

この記事の目的・目標

この記事はサポートベクターマシンの数式を理解することを主な目標に書いております。
ですので、この記事の最終目的は「不等式制約付きの２次計画問題をラグランジュの未定乗数法で解く」ところにあります。そこに向けて記事を書いていきますが、「サポートベクターマシンはどうでも良くてラグランジュの未定乗数法だけ知りたい」という方も対象となっています。

ラグランジュの未定乗数法(等式制約)

制約条件が1つの場合

【定理】
をn次元ベクトルとする。
このとき、条件 の下で関数 が極値をとる点は、



と置くと、次の式を満たす。

この①式と②式を解き連立方程式を得ることで、極値が求まります。
ここで、fを目的関数、Lをラグランジュ関数、またはラグランジアン、λをラグランジュ定数と呼びます。

解説

まず問題の意味から考えます。
g=0の下でfが極値を取るというのは、言い換えると「超曲面fと超曲面gが交わって出来る超曲面上でfが極値を取る」と言うことです。具体例を考えます。

簡単に理解するために2変数に置き換えて考えると、「x-y-z空間上の曲面fと曲面gが交差してできる曲線上で極値を取る」ことです。

制約条件 はx-y平面上では曲線として表示されます。x-y-z空間で考えると、zが定義されてないので曲線をそのまま縦方向に伸ばしたオーロラのような形状となります。

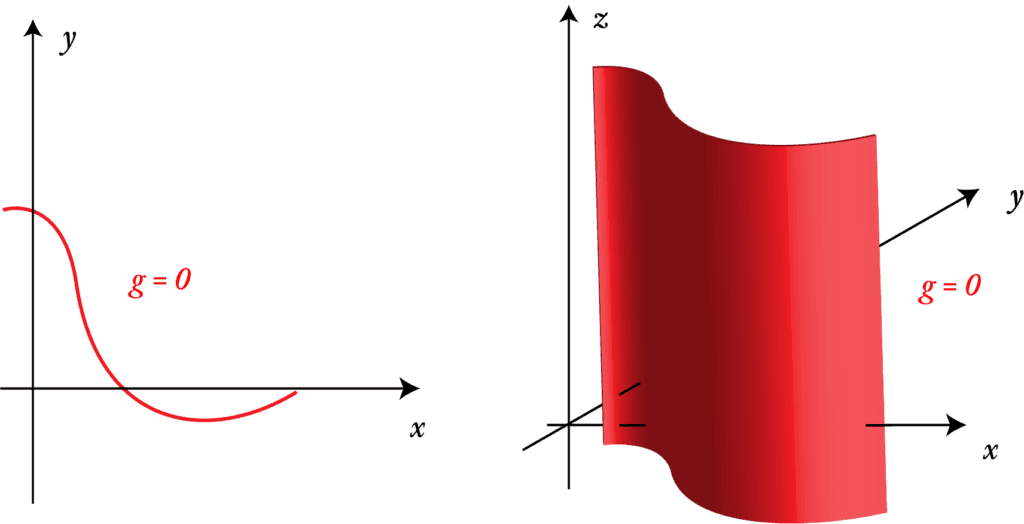
はx-y-z空間中の曲面を表します。

曲面の例を挙げます。

曲面f上で更に曲面g=0でなければならないので、
g=0の制約下でfの極値を求める問題は、このfとgが交わる曲線の極値を求める問題となります。

ここで、fとgをz軸の上から垂直に見下ろし、x-y平面上での関係を見ていきます。fを等高線として表し、gは2変数の関数なのでそのまま曲線として描きます。

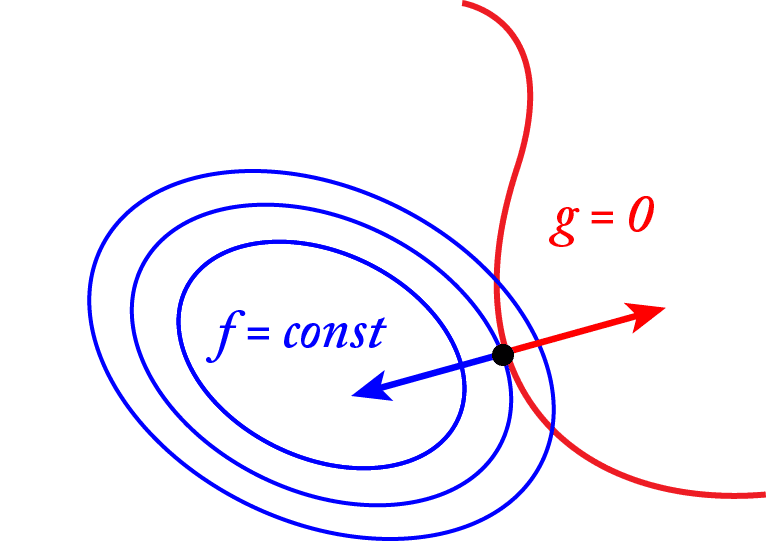
図のようにfの等高線とgは必ずどこかで接します。
図では等高線が3本しか書かれていないですが、実際には等高線は無限に引けるので、必ずどこかで接するということが納得できるかと思います。

それでは、接点における法線ベクトルを考えます。法線ベクトルnは

で表せるのでした。忘れた方は次の記事を参考にして下さい。

接点では図のように法線ベクトルが並行となります。
よって、あるスカラーλを用いて、fとgの法線ベクトルの関係は次のように書けます。

したがって、たしかに と置いたときに となって①を満たします。

②に関しては、

となって、制約条件g=0と一致します。

それでは、制約の個数を増やすことで問題を更に一般化します。

制約条件が複数の場合

【定理】
m個の条件 の下で関数 が極値を取る点は、 として、



と置くと、次の式を満たす。

ここで①および②の∇に添え字がついていますが、この演算子は次のような意味となります。

考え方は制約が1つのときと同じです。ラグランジュ定数が1つからm個に増えただけです。
①と②を解いた結果を連立方程式すれば、極値が求まります。

図形的な解釈をすると、fと全てのgが交わる超曲面上の極値を求める問題となります。

ラグランジュの未定乗数法(不等式制約)

問題を定式化します。目的関数fが極値を取る問題を、不等式条件gの元で最小値を求める問題とします。最大値を求めたい場合も、fに-1を掛けたり、fを逆数にすれば最小値を求める問題に帰着させることができます。

不等式制約下で最小値を求める

s.tはsubject toの略で「条件下で」の意味です。
このとき、次の定理が成り立ちます。

ラグランジアンを としたとき、次が成り立つ。

最後の行の3つの不等式をKKT条件といいます。

解説

KKT条件について見ていきます。 と の積は0なので、どのiに対しても片方は0になります。これは次のことを意味します。

① ならば となってi番目の制約はなくなります。
② なら となりi番目は等式制約となります。

図で解説します。
話を簡単にするためにある1つの制約gのみを考えます。

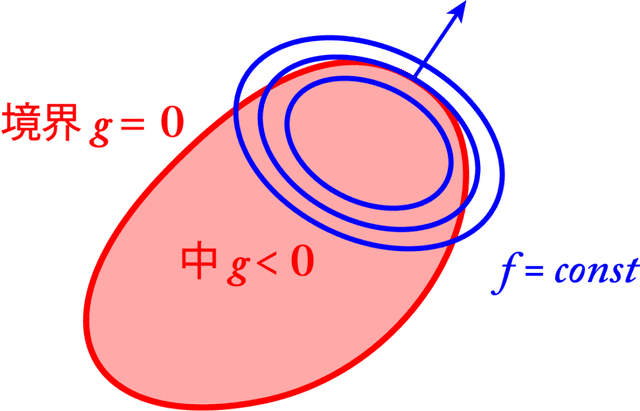
fとgの関係は2通りあります。
①領域内 での
②境界 での

① は領域の内部全体を表しており、この領域と の交わる部分は そのものなので、制約はなくなります。
つまり、ラグランジアンにおいてλ=0として制約なしの最適化にします。 となるのでラグランジアンの最小化＝ の最小化です。

②領域の境界 では等式制約と同様の制約が必要です。ラグランジアンも等式制約のときと同じ の形のものを必要としますので、λ>0となります。

KKT条件はこれらのことをまとめて表現しています。

2次計画問題

不等式制約のラグランジュの未定乗数法において２次計画問題というものを考え、目的関数fをある関数に限定します。そのためには凸関数の概念の理解が書かせません。

凸関数

次の定義を満たすものを凸関数といいます。

【定義】凸関数

解説

名前の通り、形が凸状になっている関数です。
はtは0以上1以下の値を取るという意味です。

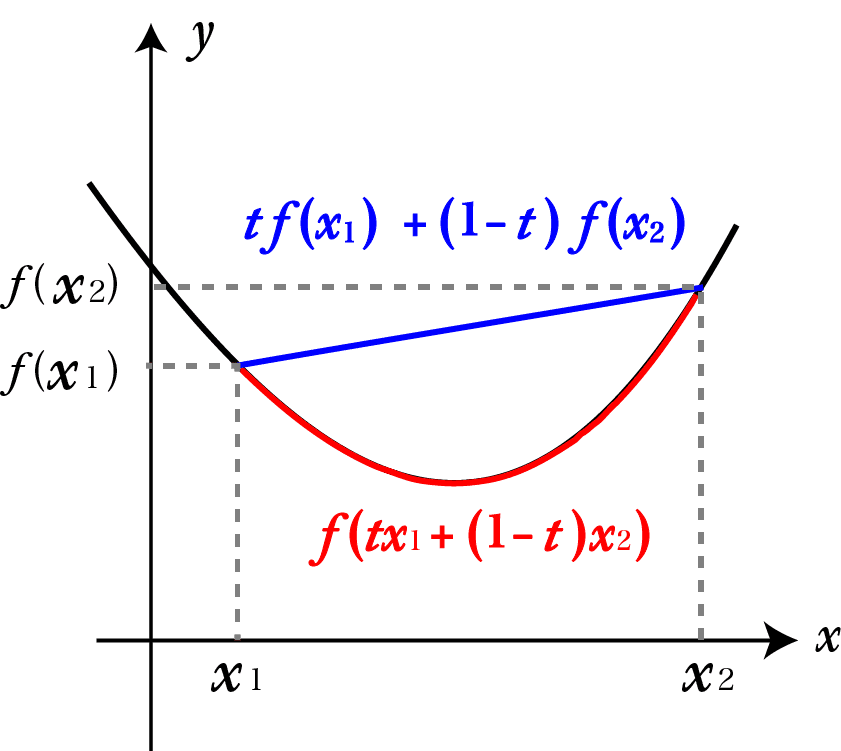
図からも分かる通り、下向きに凸状になっている(これを下に凸という)凸関数は上の定義を満たします。

2次計画問題(QP)

目的関数fが

1. ①凸関数
2. ②2次(n個すべての変数において、最大の次数が2)

のとき、 線形制約 の下でfを最小化する問題を2次計画問題(QP)と言います。

凸で2次であれば必ず極値を持ちますし、その値は目的関数fの唯一の極値かつ最大値(または最小値)となり問題が簡単になります。

QPの解法

このQPは以下の3ステップで解けます。

1つずつ見ていきます。

①ラグランジアンを作る

前節の問題に対してラグランジアンLを定義します。

②ラグランジアンを最小化するxを求める

と微分して求めます。

このxをラグランジアンに代入し、更にλについて最大化を考える問題を双対問題と言います。

【定義】QPの双対問題

この双対問題に対して、元のQPの問題を主問題と言います。

③双対問題を解く

双対問題と主問題の解は等しくなるので、この双対問題を解くと、QPが解けます。
一般的に、双対問題は主問題より制約が減り、解くのが簡単になります。

まとめ

この記事では等式制約のラグランジュの未定乗数法の説明をした後、2次計画問題の定義と解き方について解説しました。この問題はサポートベクターマシンの導出の数式で登場します。ここまで理解できて、ようやくサポートベクターマシンの数式の導出にたどり着けます。実際に次の記事でQPを利用してSVMの数式の導出を行います。

続きの記事