カーネルリッジ回帰の数式を導出・解説します。流れが詳しくわかるよう、丁寧に式変形するよう心がけております。
概要
ただの線形回帰ではデータが線形分布しているときにしか適用できませんが、高次元空間へ写像して、その空間で線形回帰をすると、元の空間では非線形回帰となります。これから説明するカーネルリッジ回帰も非線形回帰の1つです。
カーネルリッジ回帰を理解するには、リッジ回帰の理解が最低でも必要です。次のページで説明しているため、適宜参考にしてください。
数式
リッジ回帰を非線形に対応させる
データをN次元ベクトルxで表す。
元のデータxが存在する空間をΩとし、Ωから高次元特徴空間Hへの写像をϕ:Ω→Hとする。
つまり、元のデータx∈Ωが関数ϕによって、ϕ(x)∈Hに移されるとする。
ここで、ϕ(x)自体もベクトルであることに注意する。
N個のデータ{xi}i=1Nが特徴空間Hへ写像されたデータ点{ϕ(xi)}i=1Nを、次の行列でまとめて表示する。
Φ=ϕ(x1)⊤⋮ϕ(xN)⊤
ここで、元の空間Ωでの正則化項付きの2乗誤差は、次のとおりであった。詳しくは、リッジ回帰のページを閲覧されたし。
i=1∑N(yi−a⊤xi)2+λ∥a∥22⋯①
そして、これを最小化するaは、次のとおりであった。
a=(X⊤X+λI)−1X⊤y⋯②
特徴空間H上では、xiがϕ(xi)に、XがΦとなるだけなので、①及び②の特徴空間での式は、次の③及び④で表せる。
i=1∑N(yi−a⊤ϕ(xi))2+λ∥a∥22⋯③
a=(Φ⊤Φ+λI)−1Φ⊤y⋯④
カーネルに置き換える
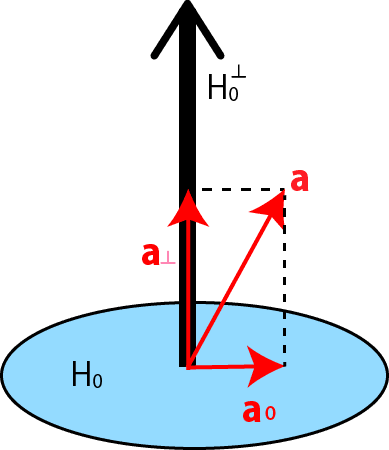
式③の内積a⊤ϕ(xi)において、{ϕ(xi)}i=1Nの張る空間をH0としたとき、H=H0⊕H0⊥と分解して、a=a0⊕a⊥(a0∈H0,a⊥∈H0⊥)とする。
よってa⊥⊥ϕ~(xi)となり、③式の内積計算において、aのa⊥成分と、それに対応するϕ(xi)の成分の項の積は直行するので内積0となり、③式の評価と関係がなくなる。したがってaはH0の元として表せれば十分である。
よってϕ(xi)の線型結合で表せれば良いので、
a=i=1∑Nciϕ(xi)
と表せる。したがって、
a⊤ϕ(xi)=j=1∑Ncjϕ(xj)⊤ϕ(xi)=j=1∑NcjKi,j
ここで、Ki,jはカーネル行列(グラム行列)の(i,j)成分である。
また、
∥a∥2=⟨i=1∑Nciϕ(xi),i=1∑Nciϕ(xi)⟩=i∑ciϕ(xi)⊤j∑cjϕ(xj)=i,j∑ciϕ(xj)⊤ϕ(xj)cj=i,j∑ciKi,jcj=c⊤Kc
よって、③式は次のように書き換えられる。
i=1∑N(yi−a⊤ϕ(xi))2+λ∥a∥22=i=1∑N(yi−j=1∑NcjKi,j)2+λc⊤Kc=∥Kc−y∥2+λc⊤Kc
この式をcで微分して、0と置くと
0Kc−λc(K−λI)c∴c=∇c(∥Kc−y∥2+λc⊤Kc)=2K⊤(Kc−y)+2λKc=K(Kc−y)+Kλc(∵K=KK⊤)=K−1K(Kc−y)+K−1Kλc=(Kc−y)+λc=y=y=(K−λI)−1y
なお、行列の微分による式変形がわからない方は、以下の記事を参考にされたし。
予測関数
よって、予測関数は次のようになる
y(x)=a⊤ϕ(x)=i∑ciϕ(xi)⊤ϕ(x)=i∑cik(xi,x)=k⊤c=k⊤(K−λI)−1y
ただしk(・,・)はカーネル関数で、それをN個並べたベクトルがkである。