【速習】高校数学で理解できる機械学習の微分と多変数関数

微分は高校生でも習いますが、機械学習で出てくる微分の理解には大学数学の知識が必要です。しかし0から大学数学の微積分を学ぼうとするのは遠回りかもしれません。この記事では機械学習で出てくる微分の必要最低限の知識をまとめます。

はじめに

前提知識

・高校レベルの微分の概念

・機械学習に出てくるベクトルの基礎知識(N次元ベクトル / ノルム / 転置 /表記方法など)
　以下の記事で短時間で学べます!!

扱うトピック

この記事で扱うトピックは次のとおりです。

• N変数関数(多変数関数)
• 1次形式と超平面
• 超平面と点の距離の公式
• 偏微分
• 勾配、ベクトルで微分
• テイラー展開

これらについてご存知のない方を対象とした記事になります。

N変数関数(多変数関数)

N変数関数とは

変数がN個ある関数のことです。

高校数学で扱う関数は、変数が1つの1変数関数 がメインで、せいぜい2変数関数 までしか扱いません。

機械学習では変数が3個以上、更に一般化されたN変数関数 を考えます。変数をこのように と並べても良いのですが、もっとスマートな記述方法があります。

N次元ベクトル を用いて のように書くことが出来ます。

高校までベクトルは「矢印」としての意味合いが強いですが、機械学習ではこのように「変数をまとめた箱、配列」として扱う方ことも多いです。ベクトル＝矢印という考えは捨てましょう。

N変数関数の幾何学的解釈

は変数がxとyの2つですので、2次元空間の直線や曲線などを表現できました。
同様にして、 は3変数なので3次元空間中の平面や曲面を表現できます。

それでは4変数 はどのような図形になるでしょうか。

答えは、4次元空間中の図形を表します。ベクトルの記事でも説明しましたが、人間は4次元空間を認識できないので具体的な形は想像すらできません。（式からなんとなくの形は分かります。）
「直線が4本垂直に交わる空間にあるなんらかの図形」という解釈をして下さい。N次元でも同様です。

N変数の平面を「超平面」、N変数の曲面を「超曲面」と言います。

ベクトルの内積でN変数関数を表現する

1次形式

N変数関数の変数 が累乗されていたり相互に積になっておらず、全て1次のケースを1次形式と呼びます。

【定義】1次形式

ただし、係数ベクトル としています。

このように1次形式では、係数ベクトルと変数ベクトルの内積の形でN変数関数を表現できます。この1次形式に定数項bを足したものを1次式と言います。

超平面

一次式を幾何学的(図形的)に考えると平面のようなものになります。1変数の場合から見ていきましょう。
ですので、直線を表す見慣れた式です。

2変数の場合は となり、3次元空間において平面を表します。

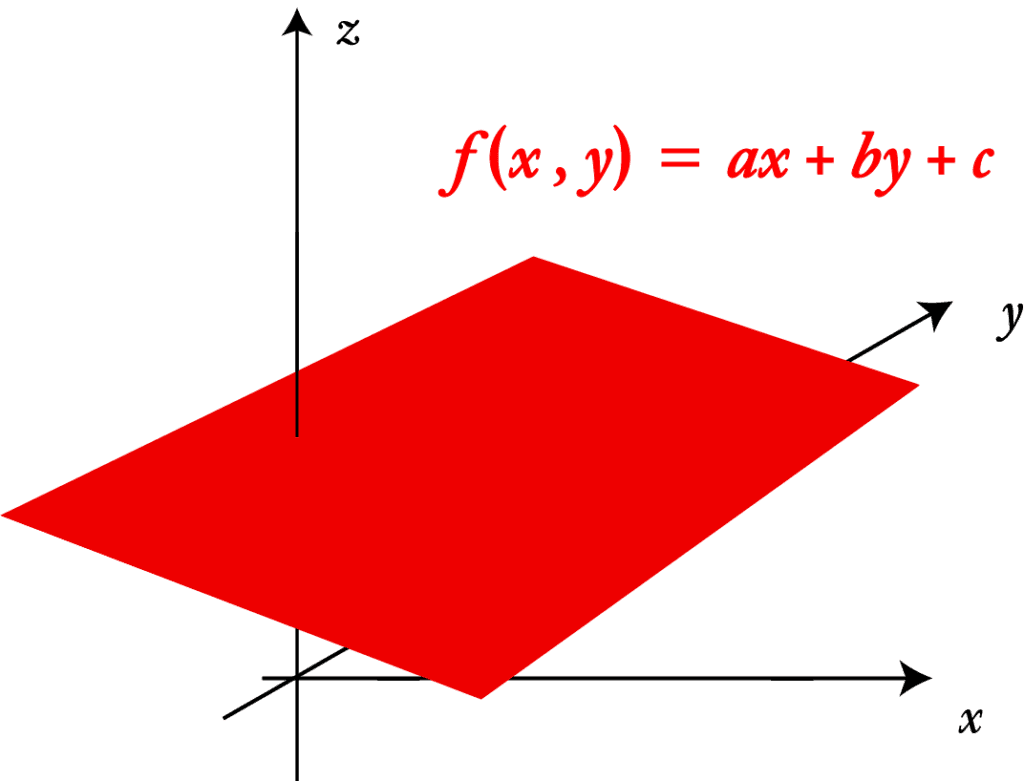
そして3変数以上のN変数では、直線→平面の延長で、平面のような図形となります。これが超平面です。

点と超平面の距離の公式

陽関数と陰関数

今まで見てきた のような関数の表記方法を「陽関数」と言います。対して、 のように片方の辺を0にする表示方法を「陰関数」と言います。
両者は相互に陽関数⇔陰関数と変換できます。具体例を見てみましょう。

直線を表す式

単にyを左辺に移動しただけですが、重要な違いが1つあります。それは変数の数です。

陰関数表示では変数の数が1つ増えます。

点と直線の距離

2次元平面上の点 から陰関数表示の直線 までの距離dは

となるのは高校で習います。これを一般化してベクトルで表現します。
係数ベクトルを 、変数ベクトルを とおけば、直線は と書けます。このとき、点 から直線までの距離は、 と置くと、

この公式はN変数の場合、すなわち点と超平面の間の距離にも成り立ちます。

【定理】点と超平面の距離
陰関数表示のN次元空間の超平面 とN次元空間中の点 との距離dは、 と置くと、

偏微分と勾配

2変数の偏微分

図で表すことのできる2変数関数 から考えましょう。

yを定数として扱い、fをxで微分したものを「xについての偏微分」といい という記号で表します。
同様に、xを定数として扱い、ｆをyで微分したものを「yについての偏微分」といい、 で表します。
∂は「ラウンド」と読みます。

具体例を挙げます。

xについての偏微分ではyは定数扱いなので、定数の微分ということで0になり消えます。
yについての偏微分でも同様です。

高階偏微分

1変数の関数に置いて、k回微分したものをk階微分といい、次の記号で表していました。

偏微分にもk階偏微分がありますが、偏微分では微分する変数が複数あるので少し注意が必要です。
2変数の2階偏微分について、次のように複数パターン存在します。

2階偏微分
① で偏微分した後、更に で偏微分する：

② xで偏微分した後、yで偏微分する：

③ yで偏微分した後、ｘで偏微分する：

④：yで偏微分した後、更にyで偏微分する：

具体例を見てみましょう

2変数の勾配

xについての偏微分、yについての偏微分を成分としたベクトルを勾配ベクトル、または単に勾配と言い、次のように表します。

∇は「ナブラ」と読みます。
具体例を挙げます。

勾配＝ベクトルで微分するということ

∇は、 と置いたとき、次の演算と等価です。

つまり、勾配はベクトルで微分するという概念になります。

勾配の性質①：値が最も大きくなる方向を表す

勾配ベクトルの向きは、その関数が最も値が増加する方向を指します。
山のような曲面で考えると、最も傾斜が急になる方向を指し示すことになります。先程から挙げている例で示すと、 のときに点 上で最も値が急激に増加する方向は となります。

勾配の性質②：極値では勾配＝0となる

1変数の微分では極値では微分＝0となりました。
その拡張のような考え方で、2変数関数の微分では極値で勾配が0となります。
曲面における極値とは、山のような曲面の場合、山頂で極大値、谷底で極小値を取ります。

注意：逆は必ずしも成り立たない

多変数関数では勾配=0でも極値とならない「鞍点(あんてん)」と呼ばれる点が存在します。
軸によって極小と極大の両方を取りうる点のことです。

N変数関数の偏微分と勾配

3変数、4変数もN変数の場合も偏微分と勾配は同様に定義できます。

【定義】N変数の偏微分
N変数関数 の1つの変数 以外を定数とみなし、その変数 で微分したものを についての偏微分といい



で表す。

【定義】N変数関数の勾配
N変数関数 の勾配は

勾配の性質も2変数のときと同様のものが成り立ちます。

勾配の公式

いくつか勾配の公式を記載します。∇がベクトルでの微分ということを意識するれば、1変数の場合とあまり変わらない演算結果が得られます。

テイラー展開

テイラー展開とは、任意の関数を1次関数や2次関数といったN次関数の無限和で表現するのもです。
テイラー展開すると、三角関数や指数関数もN次関数の和として表現することが出来ます。

1変数のテイラー展開

まずは1変数から初めます。

【定義】テイラー展開
無限階微分可能な関数が を含むとき、

を点a周りのテーラー展開という。

テイラー展開の無限和を途中で打ち切ることによって近似を表現できます。例えば無限和をn=3で早々に打ち切れば、三角関数や指数関数が1次関数、2次関数、3次関数の和だけで近似することができます。
もちろんnが小さければ近似の精度は落ちてしまいます。

多変数のテイラー展開

【定義】N変数関数のテイラー展開

このような公式は覚える必要はありません。
公式の意味するところや概念だけ理解すれば大丈夫です。テイラー展開なら「N次関数の無限和で任意の関数が表せる」という事実だけ覚えておきましょう。

まとめ

この記事では、N変数関数とは何かから始まり、偏微分や勾配についてまとめました。
定義だけではなく意味も重要で、勾配は①値が最も大きくなる方向を表す、②極値では勾配＝0となるという重要な性質を持つことについても解説しました。これらの性質は機械学習の重要なフェーズ「学習」において最も中核を担う概念となるので、是非理解して下さい。