カーネル主成分分析(カーネルPCA)の数式の導出方法を徹底解説

カーネル主成分分析(以下カーネルPCA)の数式を導出・解説します。流れが詳しくわかるよう、丁寧に式変形するよう心がけております。カーネルPCAは読んで字が如く、主成分分析(以下PCA)でカーネル法を用いたものです。PCA同様に主軸を変換しますが、この第1主軸がカーネル行列の最大固有値に対応する固有ベクトルの向きであることを数式で説明します。

概要

通常のPCAでは線形データにしか対応できないが、カーネルPCAは読んで字が如くカーネルトリックを用いるので、非線形データに対してPCAを適用することが可能となる。

PCAの数式の導出はこちらの記事から。

数式

①最適化問題導出まで

データをN次元ベクトル$\mathbf{x}$で表す。

元のデータ$\mathbf{x}$が存在する空間を$\Omega$とし、$\Omega$から高次元特徴空間$H$への写像を$\boldsymbol{\phi}:\Omega \to H$とする。
空間$\Omega$上のデータ$\left\{\mathbf{x}_i\right\}_{i=1}^N$を写像した$\left\{\boldsymbol{\phi}(\mathbf{x}_i)\right\}_{i=1}^N$に対して、特徴空間$H$での第一主軸を$\mathbf{f}$とし、この1次元上での最大分散を考える。内積の記号を$\langle\cdot , \cdot\rangle$とすると、

$\boldsymbol{\phi}(\mathbf{x}_i)$から$\boldsymbol{\phi}(\mathbf{x})$の平均を引いたものを$\tilde{\boldsymbol{\phi}}(\mathbf{x}_i)$とおくと、

より、①式は

ここで、

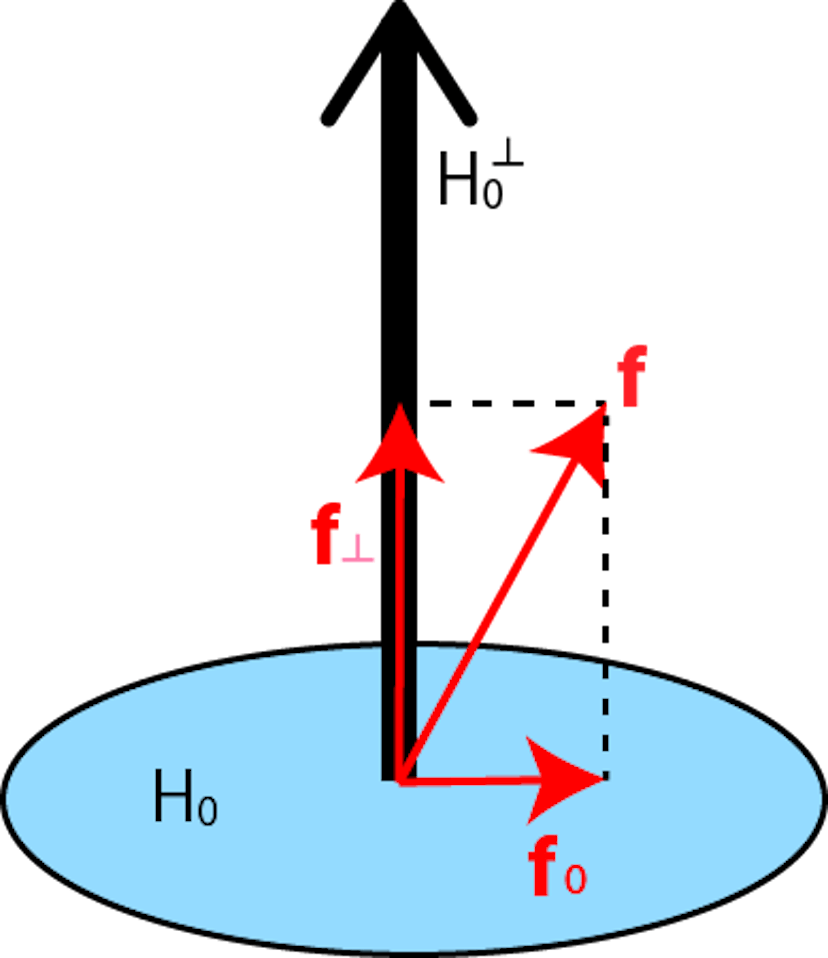
とおける。なぜならば、span{ベクトルの集合}をベクトルの集合が張る空間とすると、$H_0 = \mathrm{span}\left\{\tilde{\boldsymbol{\phi}}(\mathbf{x}_i)\right\}_{i=1}^N$としたとき、$H=H_0\oplus{H}_0^\bot$と分解でき、$\mathbf{f}=\mathbf{f}_0\oplus\mathbf{f}_\bot(\mathbf{f}_0\in{H_0},\mathbf{f}_\bot\in{H_0^{\bot}})$となる。

ゆえに$\mathbf{f}_\bot\bot\tilde{\boldsymbol{\phi}}(\mathbf{x}_i)$となり、②式の内積計算において、$\mathbf{f}$の$\mathbf{f}_\bot$成分と、それに対応する$\tilde{\boldsymbol{\phi}}(\mathbf{x}_i)$の成分の項の積は0となり、②式の評価と関係がなくなる。したがって$\mathbf{f}$は③式の形、すなわち$H_0$の元として表せれば十分である。よって②式は、

ここで、$\mathbf{K}$はカーネル行列（グラム行列）である。

また、

②最適化問題を解く

したがって、第一主軸は最大化問題

となる。ここで$\mathbf{b}=\mathbf{K}^\frac{1}{2}\mathbf{a}$とおくと、

この最適化問題のラグランジュ関数Lは

$\frac{\partial{L}}{\partial\mathbf{b}}=\mathbf{0}$とすると

となり、固有値問題に帰着する。結局、グラム行列の最大固有値に対応する固有ベクトルが第一主軸になる。

なお、行列の微分による式変形がわからない方は、以下の記事を参考にされたし。