【速習】高校数学で理解できる機械学習のベクトル

機械学習の理解にあたって最も重要なの概念はベクトルです。しかし高校で習うベクトルは基礎の基礎で、機械学習を学べるレベルのものではありません。そこで、この記事では高校レベルのベクトルを理解している人に向けて、機械学習を理解するために必要最低限なベクトルの知識をまとめます。

はじめに

前提知識

高校で習うベクトルの知識のみ。

目的

機械学習に必要なベクトルの知識を速習する。

扱うトピック

この記事では以下のトピックを扱います。

• 大学以降でのベクトルの表記方法について
• 列ベクトル・行ベクトルの違い
• 転置
• ノルム
• N次元ベクトル

これらのことについてご存知ない方を対象とした記事になります。
それでは解説していきます。

表記の違い

矢印は付けない

専門書を読むにあたって、まず気をつけたいのが表記の違いです。
高校数学でベクトルは のようにアルファベットの上に矢印をつけて表していました。

しかし大学以降でこの記述を見ることはほとんど無く、

のように小文字かつ太文字で表現するのが一般的です。書籍によって立体だったりイタリック体だったりします。

というのも、大学以降の数学では表記が統一されていません。
私は立体の太文字が好みなので、以降 で統一します。

手書きするときは縦線をつける

矢印を付けずに太文字で記述されてることは分かりました。では自分で手書きするときはどうするのでしょうか。

一般的に、縦線や斜め線を変数につけて、ベクトルでない変数(スカラ)と区別します。
以下にいくつか例を挙げます。ここらへんも厳密な記述の決まりはありません。スカラと区別されていればOKです。

成分は縦に並べて書く

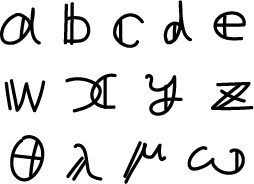
ベクトルは

のように縦に並べて描きます。これを「列ベクトル」と言います。
横に並べたベクトル は「行ベクトル」と言い、列ベクトルとは区別されます。
つまり、両者は違うものを表すことになります。詳しくは転置で解説します。

ベクトルの大きさに絶対値記号を使わない

高校までは と絶対値記号で表していましたが、大学以降では のように2重の線で囲みます。また、これをノルムと言います。詳しくは後述しています。

諸概念

転置

ベクトルを列ベクトルから行ベクトルへ、行ベクトルから列ベクトルへ変化する演算を転置と言い、次の記号で表します。

ベクトルのスタンダードが列ベクトルの縦表記なので、転置記号がついたベクトルは行ベクトルを表します。

内積

内積は高校でも習いましたが、行ベクトル、列ベクトル、転置記号を使って表現できます。

注意すべきは、行ベクトル、列ベクトルの順番で記述していることです。これは守って下さい。
行列という概念を学べばその理由が分かりますが、ベクトルは掛け算のルールがスカラより厳しいのです。

ノルム

ベクトルの大きさをノルムと言い で表します。2次元ベクトルの場合の定義は次のようになります。

4次元以上のベクトル

N次元〜4次元以上の空間〜

概念として一番とっつきにくいのがN次元についてかもしれないです。
N次元空間とは、簡単に言うならば「最大でN本の直線が垂直に交わる空間」のことです。

2次元ならばx軸とy軸の2本の軸が垂直に交わりますし、私達がいる3次元空間はそこにz軸を加えた3本の軸が交わる空間です。

では4次元とは？x-y-z軸に加えてさらにもう1本軸が垂直に交わる空間のことです。5次元なら5本の軸が垂直に交わります。…分からなくても大丈夫です。

当然、私達は4次元以上の空間を知覚認識できませんし、図で表すことも不可能ですので、具体的にN次元を想像することが出来ません。

最初のうちは具体的にイメージする必要はなく、「N本の線が垂直に交わる空間」というなんとなくの概念で捉えるだけで大丈夫です。

N次元空間の座標は、2次元や3次元のときと同様にN個の成分を のように並べ、N次元空間中のある１点を表します。

N次元ベクトル

以上を踏まえて、N次元ベクトルは次のように表されます。

【定義】N次元ベクトル

2次元ベクトルが2個の成分、3次元ベクトルが3個の成分を持っていたように、N次元ベクトルもN個の成分を持ちます。また、2次元ベクトルの成分表示が「2次元空間の原点から成分の座標へ向かう矢印」を表していたのと同様に、N次元ベクトルも「N次元空間の原点から成分の座標へ向かう矢印」を表します。

また、書籍などスペースが限られている場合に、毎回この縦長のベクトルを書いていたらスペースが足りなくなりますが、転置記号を使えば縦長のN次元ベクトルも のように1行で書けます。

N次元ベクトルの諸演算

ノルム、内積などの概念は、2次元や3次元のものをそのままN次元に拡張できます。

ノルム

内積

(ユークリッド)距離

ただ単に成分がN個に増えただけで、難しいことはありません。

まとめ

以上、機械学習で使うベクトルについて必要最低限のトピックを紹介しました。
このベクトルだけを学んでも機械学習にはたどり着けません。これに加えて多変数関数の微分についても理解が必要です。

続きの記事として、多変数関数の微分について説明します!!

(補足)さらにベクトルを学びたい人へ

N次元のベクトルは何に使う？

機械学習をするには学習データが必要です。
ほとんどの機械学習の手法が、学習データをN次元ベクトルとして利用しています。

例えば、人の身体データを学習データにしたいとします。
「身長」「体重」「体脂肪率」「顔の大きさ」「足の大きさ」「筋肉量」…など色々な特徴をデータに使うことが考えられます。
これらの数値を成分として持つベクトルを考るだけで、人の特徴のデータが数学的に扱えるようになります。

特徴を表したベクトルを特徴ベクトルといいます。ベクトルとして使うと、特徴ベクトル同士の距離が近いなら同じ人物、遠いなら別の人物、といったような判定を数学的にすることができます。

この際、矢印という概念は取っ払ったほうが分かりやすいかと思います。「矢印」と言うよりも「座標を表している」といったほうがしっくりきます。もっと簡単に、「ベクトルとはただデータ（数字)をならべた箱」という考えでも構いません。

もう1度言いますが、ベクトル＝矢印という概念は捨てて下さい。

数年前までは人手でこの特徴ベクトルを工夫して作るのがほぼマストだったのですが、特徴すら自分で学習してしまうディープラーニングという化け物が出てきました…。

ベクトルについてより詳しく学びたい方へ

大学において、ベクトルはまず初めに「線形代数」という学問の中で学びます。
線形代数を簡単に言うならば「ベクトル」と「行列」を一般化した概念を学ぶ学問です。
トピックが少なく思えますが、非常に奥が深く、それでいて抽象的な概念が多く登場します。
途中で挫折する人もいるようです。気になる方は是非調べてみて下さい。