主成分分析(PCA)の数式の導出方法を徹底解説

2024年03月13日

数学

機械学習

主成分分析(以下、PCA)の数式を導出・解説します。流れが詳しくわかるよう、丁寧に式変形するよう心がけております。PCAはデータ分布の様子をなるべく保持したままデータを低次元表現する手法です。その際主軸を変換するのですが、この主軸がデータの共分散行列の固有値問題に帰着し、最大固有値に対する固有ベクトルの向きが第一主軸となることを示します。

1 概略
2 数式
3 発展

概略

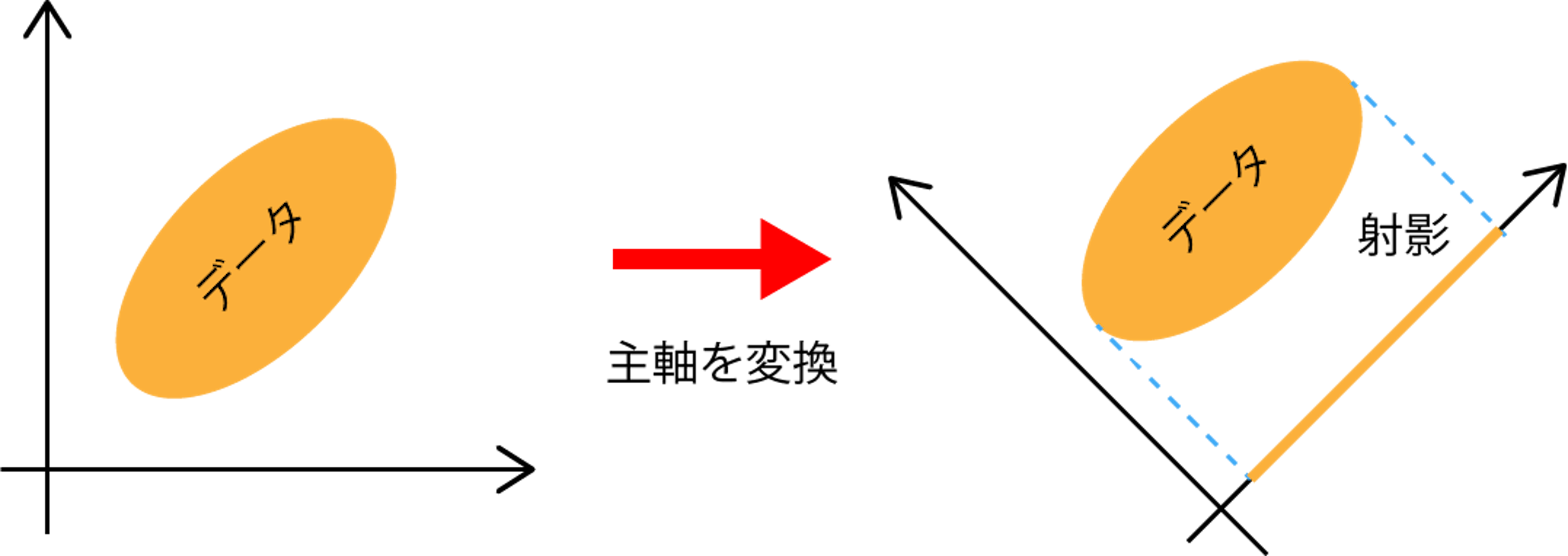
PCAでは、データ分布の分散、すなわち広がりが大きくなるような方向の主軸を見つけ、相関の少ないデータの表現を得る。この際、分散が大きい軸のみをピックアップすることで、データ分布の情報をなるべく残したまま、データの次元を削減することが可能となる。

数式

①平均ベクトルを求める

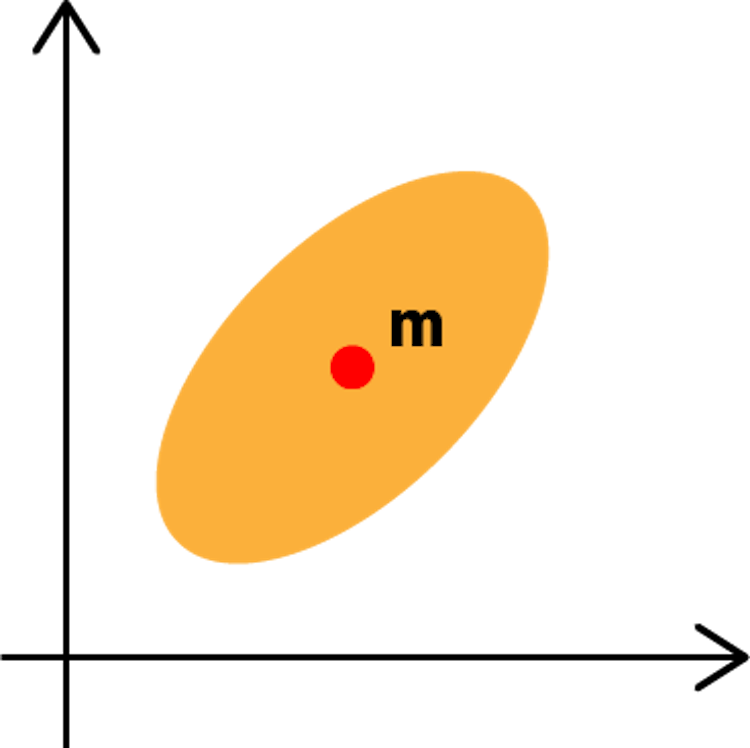
まず、 $m$ 次元空間中に、 $N$ 個のデータ $\mathbf{x}_i(i=1,…,N)$ があるとする。データの平均ベクトルmは

\mathbf{m}= \frac{1}{N}\sum^N_{i=1}\mathbf{x}_i

②データをずらす

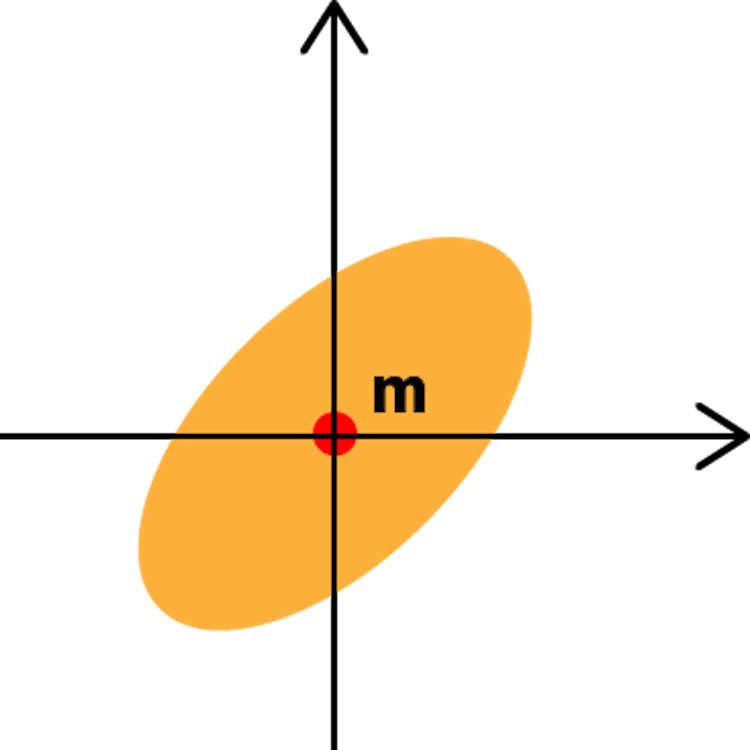
$N$ 個のデータ $\mathbf{x}_i$ を、平均ベクトル分 $\mathbf{m}$ ずらしたものを $\mathbf{r}_i$ とおくと

\mathbf{r}_i=\mathbf{x}_i-\mathbf{m}

これにより白色化し、 $\mathbf{r}_i$ の平均 $\bar{\mathbf{r}}$ は $\bar{\mathbf{r}}=\mathbf{0}$ となる。

③単位ベクトルへ射影

白色化したデータ $\mathbf{r}_i$ をある1次元単位ベクトル $\mathbf{u}$ に射影( $\mathbf{r}_i^\top\mathbf{u}$ )し、分散 $S$ を計算する。

\begin{align*} S &=\frac{1}{N}\sum_{i=1}^N(\mathbf{r}_i^\top\mathbf{u}-\bar{\mathbf{r}}^\top\mathbf{u})^2 \\ &= \frac{1}{N}\sum_{i=1}^N(\mathbf{r}_i^\top\mathbf{u})^2 \\ &= \frac{1}{N}\sum_{i=1}^N(\mathbf{r}_i^\top\mathbf{u})^\top(\mathbf{r}_i^\top\mathbf{u}) \\ &= \frac{1}{N}\sum_{i=1}^N \mathbf{u}^\top\mathbf{r}_i\mathbf{r}_i^\top\mathbf{u} \\ &= \mathbf{u}^\top\left(\frac{1}{N}\sum_{i=1}^N \mathbf{r}_i\mathbf{r}_i^\top\right)\mathbf{u} \\ &= \mathbf{u}^\top\left(\frac{1}{N}\sum_{i=1}^N (\mathbf{x}_i-\mathbf{m})(\mathbf{x}_i-\mathbf{m})^\top\right)\mathbf{u} \\ &= \mathbf{u}^\top \boldsymbol{\Sigma} \mathbf{u} \\ \end{align*}

ここで、 $\boldsymbol{\Sigma}$ は $\mathbf{x}_{i}$ の共分散行列であり、 $\mathbf{u}^\top \boldsymbol{\Sigma} \mathbf{u}$ は二次形式である。

④固有値問題に帰着

共分散行列は半正定値対称行列なので、直交対角化が可能である。つまり、共分散行列 $\boldsymbol{\Sigma}$ のある固有値 $\lambda_i$ に対する固有ベクトルを $\mathbf{u}_i$ とすると、 $\boldsymbol{\Sigma}\mathbf{u}_i = \lambda_i \mathbf{u}_i$ となるので $\mathbf{U}=[\mathbf{u}_1 \cdots \mathbf{u}_N]$ とおくと、

\begin{align*} \boldsymbol{\Sigma}\mathbf{U} &= \boldsymbol{\Sigma}\begin{bmatrix}\mathbf{u}_1 \cdots \mathbf{u}_N\end{bmatrix} \\ &= \begin{bmatrix}\boldsymbol{\Sigma}\mathbf{u}_1 \cdots \boldsymbol{\Sigma}\mathbf{u}_N\end{bmatrix} \\ &= \begin{bmatrix}\lambda_1\mathbf{u}_1 \cdots \lambda_N\mathbf{u}_N\end{bmatrix} \\ &= \begin{bmatrix}\mathbf{u}_1 \cdots \mathbf{u}_N\end{bmatrix} \begin{bmatrix} \lambda_1 & & \\ & \ddots & \\ & & \lambda_N \end{bmatrix} (\lambda_1 \ge \cdots \ge \lambda_N) \\ &= \mathbf{U}\boldsymbol{\Lambda} \\ \therefore \mathbf{U}^\top \boldsymbol{\Sigma} \mathbf{U} &= \boldsymbol{\Lambda} \end{align*}

となり、共分散行列の対角化の式となる。

ここで、 $\mathbf{u}$ を直交行列 $\mathbf{U}^\top$ により変換したものを $\mathbf{u}’$ (直交変換なので単位ベクトル)とおく。
すなわち、 $\mathbf{u}’=\mathbf{U}^\top\mathbf{u}\Leftrightarrow \mathbf{u}=\mathbf{U}\mathbf{u}’$ とすると