高校数学から理解できるSVMの数学【サポートベクターマシーン】

サポートベクターマシン(SVM)の数式の意味を「高校レベル教養」があれば理解できるよう分かりやすく解説しています。マージンの概念から始め、マージンを最大化する目的関数と双対問題、決定関数を導出するまでの式変形を細部に至るまで全て記載しています。更にハードマージンSVMから初め、ソフトマージンSVMまで解説し、スラック変数の解説もしています。

はじめに

注意事項

この記事は、SVMの数学を高校数学レベルに落とし込むのではなく、SVMに必要なレベルの数学を説明する形式になっています。なので専門書レベルの本格的な知識が身につき、他の機械学習の手法の理解にも繋がります。

前提となる知識

SVMの数学的理解には以下の基礎知識が必要です。

• 多変数関数の偏微分や勾配
• 多次元ベクトル
• 不等式のラグランジュの未定乗数法と二次計画問題

これらの概念を高校数学の知識だけで短時間で学べる記事を4つ用意しています。

①N次元ベクトルについて

②N変数関数と偏微分について

③超曲面や法線ベクトルについて

④ラグランジュの未定乗数法

本記事で分からないことがあったら、これらの記事から学べます。

ハードマージンSVM

SVMの概念とマージン

M個のm次元ベクトル がクラス1、2のいずれかに属するとして、クラス1のラベルを 、クラス2のラベルを とします。また、これらのベクトルは線形分離可能(超平面で分割できる)とします。

このm個のデータを②つのクラスに分ける超平面 の識別境界を求めるのが目的です。

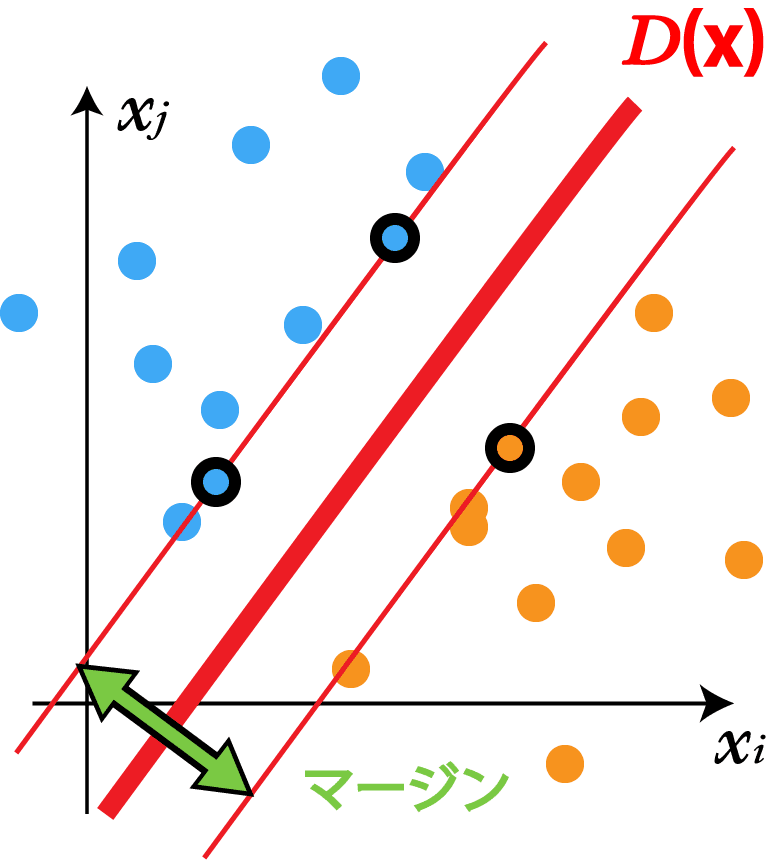
と最も近い点から までの距離を「マージン」と呼び、このマージンを最大にする を求める問題を定式化したものをハードマージンSVMと言います。

Dと最も近い点のことを「サポートベクトル」といい、図では黒フチで囲ってある点で表されています。

不等式制約の導出まで

それでは、さっそく を求める方法を解説していきます。

線形分離可能なので、一方のクラスのデータxはDの上、もう一方のクラスのデータxはDの下にあるので次を満たします。

wを使った式に置き換えると、

さらに上下をまとめて次のように書けます。

次にマージンの大きさを求めます。
Dは陰関数表示の超平面とします。よって超平面自体は と記述できます。

この超平面から最も近い点を とすると、点と超曲面の距離dは、公式より

となります。

ここで、wとbを定数倍しても距離dの大きさが変わらないことに着目します。
なので分子は

を満たします。よって、d=1となるようにwとbを適当に定数倍することができます。
すなわち、

とおけます。わざわざ1と置くのは、後の計算を楽にするためです。

最も近い点 で なので、すべての点は次の式を満たします。

これと①から、

目的関数の導出

②と③から、マージンdは

になります。

以上で役者が揃いました。
超平面Dを求める問題は、④の不等式の制約下で⑤のマージンを最大化する問題へと帰着します。

この問題を解きやすいQPに持ち込みます。 を最大化するということは、この分母 を最小化することになります。

更にこの問題は を最小にする問題と同じです。

なぜ、 と の最小化問題は同じなのか、このあたりの直感的なイメージを2次元の場合で見てましょう。

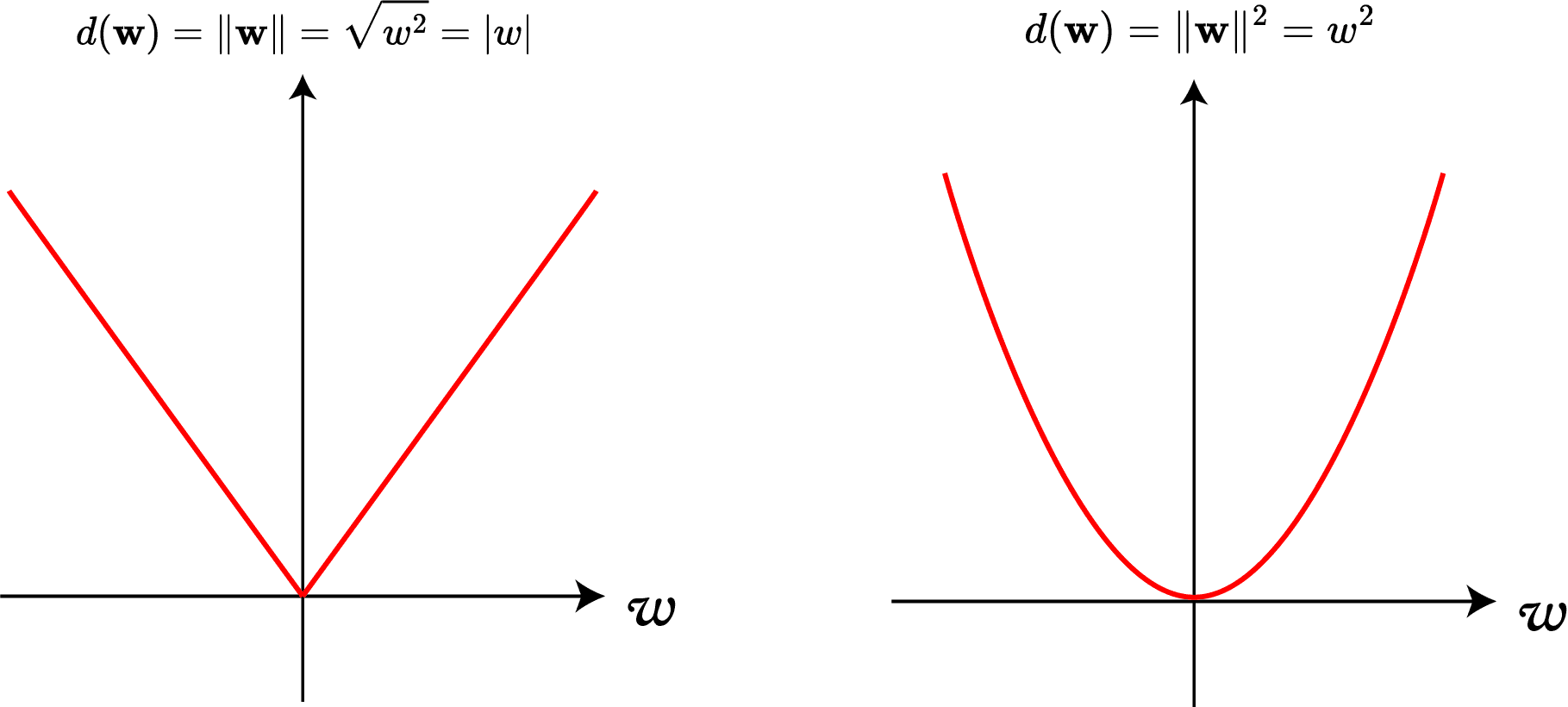
どちらの場合もdを最小にするwは原点w=0となって同じになります。
それどころか、微分可能になって極小値が簡単に求められるようになっています。

これで超平面を求めるための目的関数が得られました。

主問題から双対問題の導出

以上のことから、QPは次のようになります。

SVMのQP(主問題)

このQPを解きましょう。まずはラグランジアンを定義します。

次にwとbについて偏微分＝0をとなる点を求めます。

⑦にはbが現れないので、これは今後λとyに関する制約となります。

ここで、総和記号 の計算について1つだけ注意事項を載せておきます。
添字がiの総和記号の中で同じく添字がiの総和記号を代入する必要があるとき、片方の添字をjなどの違う文字に変更する必要があります。そうでないと、両者の演算対象が区別できず混ざってしまい、式の意味も変わってしまいます。

これを踏まえて、⑥をラグランジアンLに代入します。

よって、双対問題は

SVMのQP(双対問題)

これを満たす最適なλを求めることが、ハードマージンSVMの学習になります。この問題を解く有名なアルゴリズムにはSMOなどがありますが、今回は割愛します。
最適なλが求まったとして、話を進めます。

決定関数の導出

最適なλとw(⑥)が求まったので、これらを当初の目的である に代入します。これがSVMの識別境界となります。

SVMの識別境界

ここでSVはサポートベクトルの集合を表しています。

この式に置いて、SVとbはKKT条件から求まります。
主問題のKKT条件は

なので、 を満たすiから

として求まります。ここで、 に対応する がサポートベクトルとなります。

以上で超平面Dが算出できました。

ソフトマージンSVM

スラック変数の導入

一般的にはデータはオーバラップしていて線形分離不可能なことのほうが多いです。そのような問題に対応するため、ハードマージンSVMの制約を緩めたものがソフトマージンSVMです。

マージン最大化の考えは同じですが、いくつかのデータがマージン内に侵入していたり、あるいは識別境界を飛び越えて違うクラスに分類されてしまうことを許容します。このときの誤差をξ(非負)で定義します。

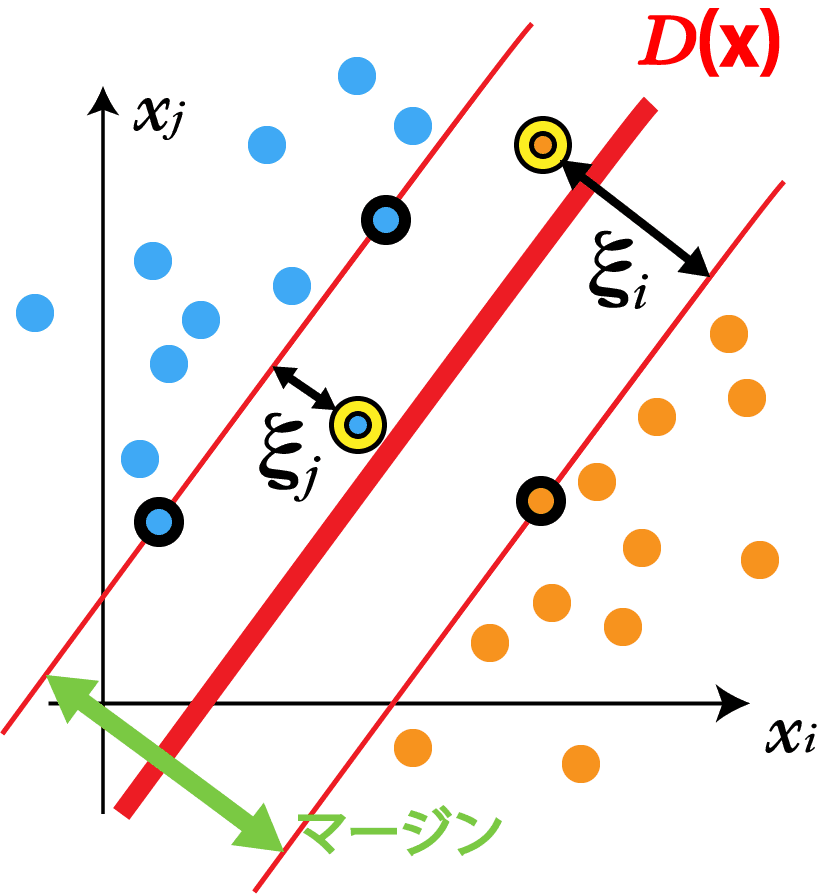
この誤差ξをスラック変数といいます。スラック変数はデータ ごとに定義されます。スラック変数を用いて、ハードマージンSVMにおける不等式制約 (④)を次のように修正します。

データ点は であればハードマージンSVMのようにマージン境界上もしくは外側に存在し、 であればマージンの内側、1より大きくなると識別境界を飛び越え誤分類されます。

目的関数の導出

この修正に伴って目的関数も考え直す必要があります。
といっても簡単で /2の最小化と同時に誤差 の最小化も考えます。
つまり、次の目的関数を最小化します。

Cやpは「誤差をどの程度厳しく最小化するか」を調整するハイパーパラメータであり、SVMのモデルを使うときに人間が試行錯誤して決める係数となります。p=1のSVMをL1SVM、p=2のSVMをL2SVMと言います。
以下L1SVMについて考えていきます。

主問題から双対問題の導出

ソフトマージンSVMの2次計画問題は、非負のスラック変数を用いて定義した⑨を⑧の不等式制約下で最小化する問題になります。

ソフトマージンSVMのQP

あとはハードマージンSVMのときと同様にこの問題を解くだけです。
ラグランジュ定数をα,βとして、ラグランジアンは次のようになります。

次に双対問題を導出するためにラグランジアンの微分=0を計算していきます。
wについての偏微分は

bについては

式中にbが出てこないので、ハードマージンSVMのときと同様に双対問題における制約となります。

最後にξについて偏微分しますが、ラクランジアンLの式中でξをベクトルで表記していませんでした(こっちのほうが式が直感通り表せるため)。ですので、あるiについてのみ偏微分して、成分の１つを求めます。

この式にξはでてこないため、これも双対問題における制約となります。

以上の結果をラグランジアンに代入すると、

となり、ハードマージンSVMのときと同じ形になることが分かります。
ここで、⑫で算出された制約 からαの取りうる値の範囲を考えます。

まず、アルファはラグランジュの係数なので、
非負なので でαが最大になるときβは0なり、その最大値は より となります。

よってαの範囲は

以上より、ソフトマージンSVMの双対問題は次のようになります。

ソフトマージンSVMの双対問題

ハードマージンSVMとの違いは、ラグランジュ乗数に上限Cがあるかないかだけになります。これを矩形制約といいます。

算出すべき超平面DもハードマージンSVMと同様です。

決定関数の導出と矩形制約について

ソフトマージンSVMの識別境界

続いて矩形制約について見ていきます。
矩形制約から について以下のことが分かります。

① のとき
はマージンより外側に存在します。
だから、KKT条件 より 、つまり誤差が0となります。

② のとき
だから、KKT条件 により 。更に なので となり、KKT条件 により 。
したがって となります。これはハードマージンSVMの制約と同じであり、 はサポートベクトルとなります。特にこのサポートベクトルとを「上限に達していないサポートベクトル」と言います。

③ のとき
より 。
更に だからKKT条件により となるので、 には誤差が生じます。
特に、 のときは識別境界手前の点となり正しく分類されますが、1以上になると識別境界を飛び越え誤分類されてしまいます。

超曲面での分離〜カーネル法へ〜

ソフトマージンSVMで分類できる対象が確かに緩和されましたが、それでも世の中どうしても解けないケースのほうが多いです。次のようなクラス分布を考えて見て下さい。

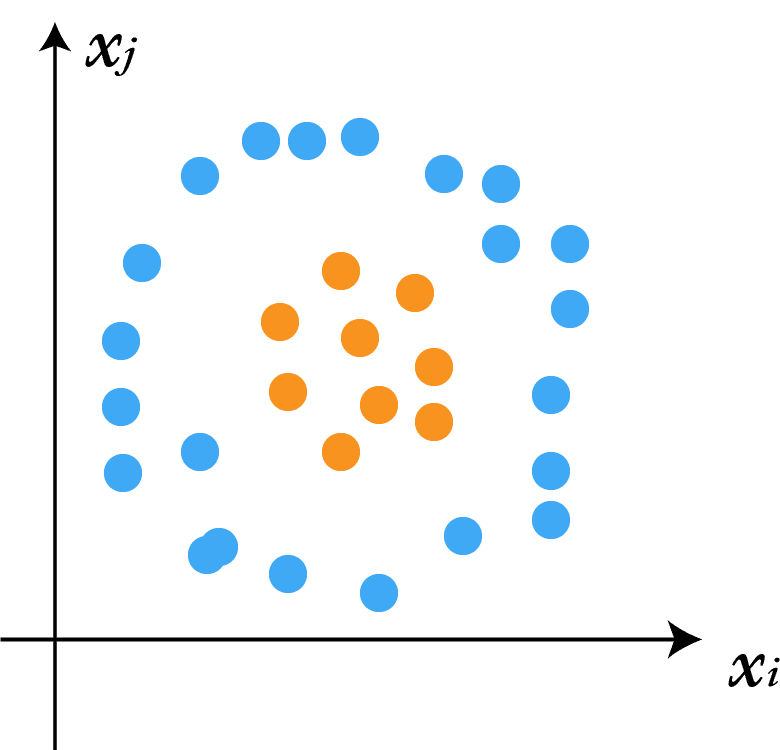
ソフトマージンSVMでも基本的に超平面(直線)による分類です。
このようなクラス分布を分割するには円形の識別境界が必要になります。

この問題をSVMでも解けるようにするのがカーネル法なのですが、記事が長くなりましたので別の記事でまとめます。カーネル法を利用した識別境界の数式のみ記載します。

カーネル法を利用したSVMの識別境界

まとめ

以上、ハードマージンSVMとソフトマージンSVMの数学を0から識別境界である判別関数の導出まで丁寧に説明しました。ハードマージンSVMもソフトマージンSVMも最終的な式が等しくなることも示しました。式変形を細部まで書いたので読み応えはあると思いますが、その分理解しやすくなっているかと思います。